C-Programming A Practical Approach
B.A./B.Sc. Part-II [Mathematics]
Group B (All Programs)
Numerical Integration
Write a C program to evaluate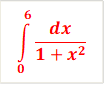 
By using:
1.Trapezoidal Rule
2.Simpson’s 1/3 Rule
3.Simpson’s 3/8 Rule
4.Weddle’s Rule
Experiment No. B-1: Trapezoidal Rule
Source Code:
/*C Program: Trapezoidal Rule */
#include<stdio.h>
#include<conio.h>
float fun(float x);
void main()
{
float x0,xn,h,sum,r;
int i, n;
clrscr();
printf(“Enter the Lower Limit of Integral:\n”);
scanf(“%f”,&x0);
printf(“Enter the Upper Limit of Integral:\n”);
scanf(“%f”,&xn);
printf(“Enter the segments width: \n “);
scanf(“%f”,&h);
n=int(xn-x0)/h;
sum=(fun(x0)+fun(xn))/2.0;
for(i=1; i<n; i++)
{
sum=sum +fun(x0+i*h);
}
r=sum*h;
printf(“\nValue of integral using trapezoidal rule is=%f\n”,r);
getch();
}
/* function definition fun() */
float fun(float x)
{
return(1.0/(1.0+x*x));
}
Output:
Watch Video tutorial (Trapezoidal Rule)
Experiment No. B-2: Simpson’s 1/3 Rule
Solution: formula of Simpson’s 1/3 rule:
Here n is even number and h = (xn-x0)/n
Source Code:
/*C Program: Simpson’s(1/3) Rule*/
#include<stdio.h>
#include<conio.h>
void main()
{
float f(float x);
float l,u,h,sum =0.0,result;
int i,n;
clrscr();
printf(“\nEnter lower limit of the integral:”);
scanf(“%f”,&l);
printf(“\nEnter upper limit of the integral:”);
scanf(“%f”,&u);
printf(“\nEnter the number of segments:”);
scanf(“%d”,&n);
if(n%2!=0)
printf(“\nNumber of segments not even number\n”);
else
{
h=(u-l)/n;
sum=f (l)+f(u);
for(i=1; i<n; i++)
{
if(i%2==0)
sum=sum+2.0*f (l+i*h);
else
sum=sum+4.0*f(l+i*h);
}
result =(h/3.0)*sum;
printf(“\n\nValue of integral is=%f\n”, result);
}
getch();
}
/* function definition */
float f(float x)
{
return(1.0/(1.0+x*x));
}
Output:
Watch Video tutorial (Simpson’s 1/3 Rule)
Experiment No. B-3: Simpson’s 3/8 Rule
Solution formula of Simpson’s 3/8 Rule:
Note: The no. of sub-intervals n, should be a multiple of 3 for this method.
Source Code:
/*C Program: Simpson’s(3/8) Rule*/
#include<stdio.h>
#include<conio.h>
#include<math.h>
void main()
{
float f(float x);
float l,u,h,sum =0.0,result;
int i,n;
clrscr();
printf(“\nEnter lower limit of the integral:”);
scanf(“%f”,&l);
printf(“\nEnter upper limit of the integral:”);
scanf(“%f”,&u);
printf(“\nEnter the number of segments (Multiple of 3):”);
scanf(“%d”,&n);
h=fabs(u-l)/n;
sum=f(l)+f(u);
for(i=1; i<n; i++)
{
if(i%3==0)
sum=sum+2.0*f(l+i*h);
else
sum=sum+3.0*f(l+i*h);
}
result =(3*h/8)*sum;
printf(“\n\nValue of integral is=%f\n”, result);
getch();
}
/* function definition */
float f(float x)
{
return(1.0/(1.0+x*x));
}
Output:
Watch Video tutorial (Simpson’s 3/8 Rule)
Experiment No. B-4: Weddle’s Rule
Solution formula of Weddle’s Rule:
Here n is number (sub-interval) and h = (xn-x0)/n
Source-Code:
/*C Program: Weddle’s rule*/
#include<stdio.h>
#include<conio.h>
#include<math.h>
void main()
{
float f(float x); /* Function Prototype declaration */
float l,u,h,sum =0.0,result; /* variable declaration */
int i,n,m;
clrscr();
printf(“\n Enter lower limit of the integral:”);
scanf(“%f”,&l);
printf(“\n Enter upper limit of the integral:”);
scanf(“%f”,&u);
printf(“\n Enter the number of segments:”);
scanf(“%d”,&n);
h=fabs(u-l)/n;
printf(“\n h= %f\n”,h);
m=n/6;
if(n%6==0)
{
for(i=1;i<=m;i++)
{
sum=sum+(3*h/10)*((f(l)+5*f(l+h)+f(l+2*h)+6*f(l+3*h)+
f(l+4*h)+5*f(l+5*h)+f(l+6*h)));
l=l+6*h;
}
printf(“\nResult is : %f\n”,sum);
}
else
{
printf(“Weddle’s rule is not applicable\n”);
}
getch();
}
/* function definition */
float f(float x)
{
return(1.0/(1.0+x*x));
}
Output:
Watch Video tutorial ( Weddle’s Rule)
How to Run above Program?
We can run/execute above programs in Turbo C/C++ (MS-DOS Based version) or Dev C++/Visual Codes programs.
If you run in Turbo C Compiler then type the above source code then run the program.
And if you Run in other Compiler then change in the above code void main() to int main() and remove #include <conio.h> and clrscr() , getch() functions and add return 0; statement at end of the void main() function (before closing }).
e,g.
In Turbo C/C++ compiler In Dev C/C++ and Others IDEs(VC)
#include<stdio.h> #include<stdio.h>
#include<conio.h>
void main() int main()
{ {
variable declaration part; variable declaration part;
clrscr();
– – – – – –
Executive Part; Executive Part;
– – – – – –
getch(); return 0;
} }
Watch Video tutorial ( How to Run C Program)