ü Tree is a nonlinear data structure and acyclic connected graph that has no loops or cycle.

ü Tree represents a hierarchical relationship among the various data elements.

ü Each data element in a tree is called a node. The topmost node of the tree is called a root.

ü The nodes in a tree are connected to other nodes through edges.

 

 

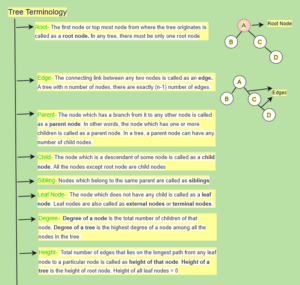
Tree Terminology

 

Tree Traversal-

 

Tree Traversal means of visiting each node in a tree data structure exactly once.

 

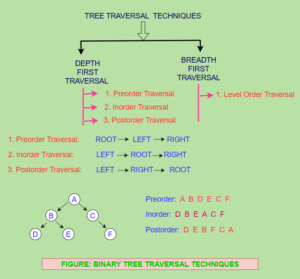
There are two type of Binary Tree traversal techniques-

(a) Depth First Traversal:

Following three traversal techniques fall under Depth First Traversal-

1.  Preorder Traversal

2.  Inorder Traversal

3.  Postorder Traversal

Depth first Traversal is stack based.

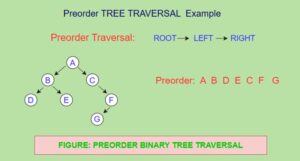
1. Preorder Traversal:

To traverse a non-empty binary tree in Preorder, we perform the following three operations.

1)  Visit the Root node

2)  Traverse the left subtree in Preorder

3)  Traverse the right subtree in Preorder

 

 

ALGORITHM:PRE-ORDER TRAVERSAL (Recursive Algorithm)

preorder (PTR)  [Let PTR contain the address of the root node]

 

if (PTR != NULL) then

     write PTR->DATA

     preorder (PTR->LEFT)

     preorder (PTR->RIGHT)

endif

exit

 

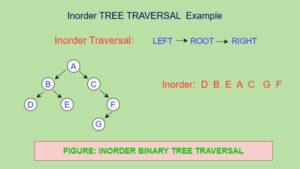
2. Inorder Traversal:

To traverse a non-empty binary tree in Inorder, we perform the following three operations.

1)  Traverse the left subtree in Inorder

2)  Visit the Root node

3)  Traverse the right subtree in Inorder

 

 

ALGORITHM: IN-ORDER TRAVERSAL (Recursive Algorithm)

 

inorder (PTR)  [Let PTR contain the address of the root node]

 

if (PTR != NULL) then

     inorder (PTR->LEFT)

     write PTR->DATA

     inorder (PTR->RIGHT)

endif

exit

 

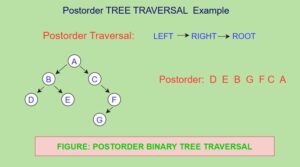
3. Postorder Traversal:

To traverse a non-empty binary tree in Postorder, we perform the following three operations.

1)  Traverse the left subtree in Postorder

2)  Traverse the right subtree in Postorder

3)  Visit the Root node

 

 

ALGORITHM: POST-ORDER TRAVERSAL (Recursive Algorithm)

 

postorder (PTR)  [Let PTR contain the address of the root node]

 

if (PTR != NULL) then

     postorder (PTR->LEFT)

     postorder (PTR->RIGHT)

     write PTR->DATA

 endif

exit

 

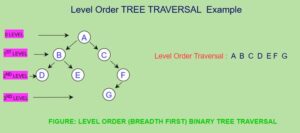
(b) Breadth First Traversal:

·       Breadth First Traversal is also called as Level Order Traversal.

·      In this technique, first we process all the nodes of a tree level by level (0^th Level then 1^st Level
and so on).

·       Level order is Queue based.